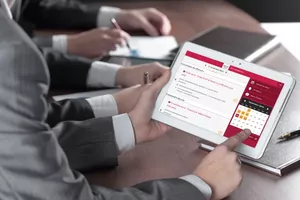
2.2 L'investigation épidémiologique des effets de faibles doses est impuissante à déterminer des facteurs de risque utilisables
Cet état de fait est particulièrement fâcheux puisque ce qu'il est convenu d'appeler les "faibles doses" est justement le domaine d'action privilégié de la radioprotection... Je n'entre pas ici dans le détail de ce que l'on peut appeler « faibles doses » ; sachons simplement qu'il s'agit grosso modo des doses inférieures à 0,1-0,2 Gy.
L'incapacité de l'épidémiologie à fournir directement des conclusions pratiques dans les faibles doses résulte des incertitudes inhérentes à toute investigation de nature statistique lorsque l'effet que l'on cherche à mettre en évidence est pratiquement confondu avec le « bruit de fond naturel ». Ces incertitudes sont sensibles tant pour ce qui concerne le caractère significatif des conclusions de l'étude (notion de « puissance statistique ») que pour ce qui concerne la précision numérique des estimateurs calculés pour le risque étudié (notion d' « intervalle de confiance » pour ces estimateurs).
2.2.1 La puissance statistique des études épidémiologiques est insuffisante aux faibles doses
La notion de « puissance statistique » est plutôt difficile à expliquer. Commençons donc d'abord par présenter brièvement le phénomène avant d'en voir les conséquences lorsque l'on étudie les effets des faibles doses.
L'objectif d'une étude épidémiologique est de déterminer pour une certaine population (public en général, travailleurs, enfants...) le risque supplémentaire causé par l'exposition aux rayonnements ionisants. Idéalement l'étude devrait pouvoir comparer l'ensemble des individus exposés à l'ensemble des individus non exposés. En général, l'étude ne peut pas porter sur toute cette population : le chercheur est conduit à n'en retenir qu'une partie, alors qu'il souhaite conclure erga omnes. Par exemple on peut chercher à déterminer les risques des rayonnements ionisants à partir des survivants des bombardements d'Hiroshima et Nagasaki, ou bien des travailleurs de l'industrie nucléaire, ou bien de telle ou telle catégorie de malades traités par rayonnements, chacun de ces groupes n'étant qu'une facette particulière de la population mondiale.
Chaque étude n'est donc qu'un test parmi beaucoup d'autres tests possibles. Selon la façon dont la cohorte étudiée a été constituée, il est possible que l'on détecte un risque alors qu'il n'existe pas en fait ; de même il est possible que l'on ne détecte pas de risque alors qu'il existe en fait. Quelle que soit la nature de la conclusion tirée par le chercheur, celle-ci peut donc être exacte ou fausse. Il est impossible d'affirmer qu'une étude donnée fournit un résultat vrai ou faux ; en revanche les caractéristiques méthodologiques de cette étude permettent de quantifier les « chances » d'obtenir un résultat vrai ou faux. Un résultat est dit significatif au plan statistique si, en l'absence de toute cause sous-jacente, il ne peut pas survenir plus de une fois sur 20 du fait du hasard. La puissance statistique d'une étude mesure la probabilité de détecter un risque significatif lorsqu'il existe.
Le schéma suivant devrait exposer les choses de façon plus intuitive. Y sont représentées la population exposée et la population non exposée. Les points représentent l'effet étudié c'est-à-dire en l'occurrence l'induction d'un cancer mortel ; ils sont répartis de façon aléatoire dans les deux populations et sont plus nombreux dans la population exposée que dans la population non exposée (environ 2 fois). On en déduit que dans la situation schématisée ici, le risque relatif est d'environ 2.

L'épidémiologiste ne peut matériellement s'intéresser qu'à une partie des populations exposée et non exposée. J'ai représenté par des ellipses trois façons de constituer les échantillons au sein de chaque population. On voit ainsi que :
- selon les échantillons constitués, le chercheur mesurera 3, 4 ou 5 cas dans l'échantillon exposé et 1, 2 ou 3 cas dans l'échantillon non exposé ; les points sont pourtant répartis à peu près également sur chacune des deux surfaces ;
- donc il pourra légitimement calculer un coefficient de risque compris entre 5÷1, soit 5, ou 3÷3 soit 1 ; selon les hasards de l'étude, le chercheur pourra ainsi conclure qu'il n'existe pas de risque supplémentaire ou bien que le risque est quintuplé dans la population exposée.
Par ailleurs il est possible d'inférer de ce schéma sommaire quelques autres enseignements :
- si la surface des ellipses (c'est-à-dire taille des échantillons étudiés) augmente, les fluctuations absolues au sein de chaque échantillon diminuent : les évaluations du risque ont moins de chance d'être très éloignées de la vraie valeur du risque ;
- si la valeur du risque relatif est plus faible (le nombre de points représentés dans la population exposée se rapproche de celui de la population non exposée), les fluctuations comparées s'accroissent entre les mesures pratiquées sur les échantillons exposés et sur les échantillons non exposés ; il est donc plus difficile de mettre en évidence le risque étudié ;
- un effet similaire peut être observé si l'on réduit la taille de l'échantillon exposé par rapport à la taille de l'échantillon non exposé.
En résumé la puissance statistique d'une étude est d'autant plus grande que la taille des échantillons étudiés est élevée, le risque relatif est élevé, la proportion de personnes exposées dans la population totale est élevée.
Or justement, dans le cas des rayonnements ionisants, le risque relatif est plus réduit aux faibles doses qu'aux doses élevées. Donc toutes choses égales par ailleurs, la puissance statistique des études « faibles doses » est inférieure à celle des études « fortes doses ». Dans un rapport rédigé en 1995 par le National Radiological Protection Board pour le compte de l'IPSN (8 ( * )) , on trouve une illustration numérique de cette différence. Elle compare la puissance statistique attendue dans la détermination du risque de leucémie d'une part, de cancer d'autre part, pour deux études que l'on pourrait conduire à partir des données fournies par les survivants d'Hiroshima et Nagasaki :
- si l'on s'intéresse au groupe des personnes exposées dans la fourchette [0,2-0,49] Gy, on peut calculer que l'on a 71 % de chances de détecter une augmentation significative du risque de leucémie (s'il existe) d'une part, 78 % de chances de détecter une augmentation significative du risque de cancer radioinduit (s'il existe) d'autre part ;
- si l'on s'intéresse au groupe des personnes exposées dans la fourchette [0,01-0,05] Gy, on peut calculer que l'on a 7 % de chances de détecter une augmentation significative du risque de leucémie (s'il existe) d'une part, 8 % de chances de détecter une augmentation significative du risque de cancer radioinduit (s'il existe) d'autre part ;
Calculable à l'avance, la puissance statistique d'une étude épidémiologique peut être utilisée de diverses façons. Par exemple, connaissant un ordre de grandeur du risque à mettre en évidence, on peut déterminer le nombre de personnes qu'il sera nécessaire de suivre afin de mettre en évidence ce risque de façon significative. En sens inverse, pour une cohorte d'effectif déterminé, il est possible de déterminer le risque relatif minimal que l'on pourra détecter avec une chance raisonnable. Enfin, connaissant l'effectif de la cohorte et l'ordre de grandeur du risque à étudier, on peut calculer la probabilité de détecter ce risque de façon statistiquement significative ; c'est l'objet des calculs faits par le NRPB, présentés ci-dessus.
Deux remarques intéressantes peuvent être soulignées, puisqu'elles vont à encontre du « bon sens » quotidien :
- une étude ayant une puissance statistique insuffisante n'est pas inutilisable : elle peut fournir une limite supérieure du risque étudié, éliminer des hypothèses extrêmes ou resserrer la fourchette des estimations ;
- augmenter la taille de l'échantillon non exposé est intéressant : en effet il contribue lui aussi à apporter de l'information utile à l'étude épidémiologique.
2.2.2 Une puissance statistique insuffisante va de pair avec des déterminations peu précises des coefficients de risque
En définitive la puissance statistique mesure pour le chercheur le risque de se tromper lorsqu'il conclut sur l'existence ou l'inexistence d'un effet. De son côté la valeur numérique du risque calculé est elle même entachée d'une incertitude, due au fait que le risque calculé dans une enquête épidémiologique n'est qu'une estimation du risque véritable dans la population.
Cette estimation s'accompagne d'une certaine variabilité : il est probable que la valeur du coefficient de risque déterminée par l'étude sera légèrement différente de la valeur véritable du coefficient de risque dans la population. Compte tenu des caractéristiques de l'étude et de la population globale, il est possible de déterminer une fourchette de valeurs, appelée intervalle de confiance, à l'intérieur de laquelle le véritable coefficient de risque se situe vraisemblablement. Plus l'intervalle de confiance est étroit, plus la détermination numérique du coefficient de risque est précise. Toutes choses égales par ailleurs, l'intervalle de confiance sera d'autant plus étroit que l'effectif étudié est élevé.
On utilise généralement un intervalle de confiance à 90 % ou à 95 %. Cela veut dire que la valeur réelle du coefficient a 90 % ou 95 % de chances de se trouver dans la fourchette déterminée. Un exemple tiré des études conduites sur les survivants d'Hiroshima et Nagaski permettra d'éclairer concrètement ces considérations.
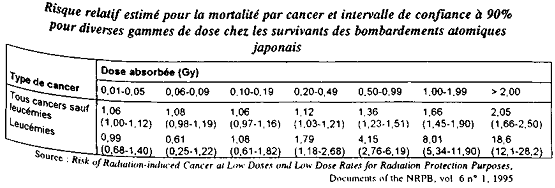
Pour diverses fourchettes de dose absorbée et les deux grandes catégories de cancers radioinduits, le tableau fait apparaître les valeurs du risque relatif avec leur intervalle de confiance à 90 %. Une valeur du risque relatif égale, voire inférieure, à 1 indique que les rayonnements n'ont pas eu d'impact visible sur l'induction d'un cancer. Regardons tout d'abord la première ligne du tableau, relative aux cancers autres que leucémies :
- on remarque que toutes les valeurs du risque relatif sont supérieures à 1 : on pourrait en déduire que les doses les plus faibles (0,01-0,05) Gy induisent un risque détectable conduisant à un excès de cancer d'environ 6 % par rapport à une population non exposée ; la conclusion serait similaire pour les autres fourchettes de dose indiquées dans le tableau ;
- cependant l'examen des intervalles de confiance amène à reconsidérer cette conclusion : pour la fourchette de dose (0,01-0,05) Gy, l'intervalle de confiance est (1,00-1,12) ; ceci veut dire que, si 1,06 est bien la valeur la plus probable du risque, en fait celui-ci a 90 % de chance de se situer entre 1,00 et 1,12 ; il est tout à fait possible que la valeur réelle du risque relatif dans cette fourchette de dose soit en fait égale à 1,00, donc que l'exposition au rayonnement n'entraîne pas de risque de cancer radioinduit excédentaire ;
- cette conclusion partielle est renforcée par l'examen de l'intervalle de confiance associé à la valeur du risque pour la fourchette (0,06-0,09) Gy : on voit que, si 1,08 est bien la valeur la plus probable du risque, la valeur réelle du risque a 90 % de chance de se situer entre 0,98 et 1,19 ; on dit alors que le résultat n'est pas significativement différent de 1 car il est impossible de déterminer précisément si l'exposition au rayonnement a provoqué un risque excédentaire (valeur supérieure à 1) ou non (valeur inférieure ou égale à 1) ;
- la conclusion est identique pour la fourchette de dose (0,10-0,19) Gy puisque l'intervalle de confiance à 90 % encadre la valeur 1 ;
- on ne commence à détecter d'excès significatif de cancer que pour des doses supérieures à 0,20 Gy puisque c'est à partir de la fourchette de dose (0,20-0,49) Gy que les intervalles de confiance excluent la valeur 1.
L'étude de la ligne relative aux leucémies amène à des conclusions similaires : 1/ le simple examen des valeurs estimées pour le risque pourrait faire croire que celui-ci est plus faible pour une population exposée à des doses comprises entre 0,06 et 0,09 Gy que pour une population non exposée ; 2/ en fait l'intervalle de confiance associé à cette valeur montre qu'on ne peut pas exclure que la valeur réelle du risque soit supérieure à 1 ; 3/ en définitive l'examen de tous les intervalles de confiance montre qu'un excès de leucémies n'est significatif que pour des doses supérieures à 0,20 Gy.
En résumé, l'étude de ce tableau montre que pour des doses « trop » faibles - en l'occurrence inférieures à 0,20 Gy, l'intervalle de confiance est trop important pour que l'on puisse déterminer de façon précise si un risque existe.
Le tableau est fondé sur les données arrêtées en 1985. Or le suivi des populations japonaises se poursuit, ce qui implique que la puissance de l'étude augmente. Les prochains résultats devraient ainsi permettre de réduire l'amplitude des intervalles de confiance. Les estimations du risque seraient alors plus précises, et certains spécialistes s'attendent à ce que l'on puisse mettre en évidence un risque excédentaire de façon significative dans la fourchette de dose (0,10-0,19) Gy.
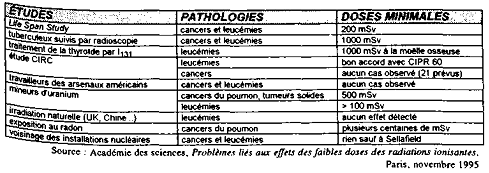
Le rapport de l'Académie des sciences publié en 1995 dresse un tableau fort intéressant, qui montre les doses minimales en-dessous desquelles les études épidémiologiques majeures sont actuellement incapables de déceler un excès statistiquement significatif.
Limites inférieures de sensibilité
des études épidémiologiques
(en l'état des
connaissances en 1995)
Puissance statistique insuffisante, imprécision des coefficients de risque calculés : la voie d'une étude directe des effets des « faibles doses » semble pour le moins hasardeuse. Est-ce à dire que la science soit impuissante à répondre aux besoins de la protection radiologique ?
Non, mais elle doit pour cela emprunter des chemins détournés.
* 8 NRPB, Risk of Radiation-induced Cancer at Low Doses ond Low Dose Rates for Radiation Protection Purposes. Documents of the NRPB, vol 6 n° 1, 1995